An Introduction to Approximate Bayesian Computation
Introduction
With the term Markov Chain Monte Carlo, notably referred as MCMC, we refer to statistical methods that allow to generate a dependent sample from a probability distribution. MCMC utilises a Monte Carlo method based upon Markov Chains, and its main application is primarily in Bayesian statistics to provide samples from the posterior distribution. MCMC can be traced back to Metropolis et al. (1953) and Hastings (1970), but it became very popular after the publication of the Gibbs Sampler by Geman and Geman (1984).
An important aspect of the applicability of this family of methods is that the likelihood function must be somehow tractable. However, there are many situations where we are not able to write it down explicitly: in these situations, we therefore need to rely on different methods.
Approximate Bayesian Computation to the Resque!
Among many, Approximate Bayesian Computation (ABC) has the key benefit over MCMC of not requiring a tractable likelihood. It was introduced in the context of statistical analysis of population genetics by Tavare et al. (1997), and it became very popular thanks to Christian Robert and colleagues - for a general introduction, I strongly encourage to read the following paper.
The aim of this post is to expose you to the plain vanilla ABC algorithm. I will provide a practical example - written in Python - to give you a better understanding of the proposed methodology. In particular, we will try to replicate the example provided by Dempster et al. (1977) under the ABC framework.
The Framework
Let $x^{\ast}$ denote the observed data which is assumed to be generated by a generic model with parameters $\theta$. From Bayes’ Theorem, we all know that the posterior distribution is proportional to the likelihood times the prior, namely
\[\pi\left(\theta \vert x^{\ast} \right) = \frac{\pi(x^{\ast} \vert \theta) \pi(\theta)}{\pi(x^{\ast})} \propto \pi(x^{\ast} \vert \theta) \pi(\theta)\]Under this framework, we are able to choose the prior distribution so that everything is tractable and easy to work with - namely, we are able to estimate the sufficient statistic. In particular, using a rejection algorithm, we can produce iid samples from $\pi\left(\theta \vert x^{\ast}\right)$ without the need to evaluate $\pi\left(x^{\ast} \vert \theta\right)$.
Standard statistical inference theory also tells us that to estimate the posterior distribution of $\theta$ all we need to know is the sufficient statistic of the data. Let T(x) denote a sufficient summary statistic of the data x.
The algorithm
Typically, when ABC is used it is not always possible to identify sufficient statistics, since the likelihood can not be written down.
Notably, however, to generate samples from the posterior distribution, we need to approximate it. Let $d(\cdot, \cdot)$ denote a distance metric. Then for $\epsilon \geq 0$, define the $\epsilon$ approximate posterior distribution, $\pi_{\epsilon}\left(\theta \vert x^{\ast}\right)$, as follows: \(\pi_{\epsilon}\left(\theta \vert x^{\ast}\right) \propto \pi(\theta) \int_{\Lambda} \pi(T(x) \vert \theta) d\theta\)
where $\Lambda := \left( x: x \in d(T(x), T(x^{\ast}) \leq \epsilon)\right)$.
To obtain a sample from $\pi_{\epsilon}\left(\theta \vert x^{\ast}\right)$, we use the following algorithm, that is defined here as plain-vanilla ABC Algorithm:
- Simulate $\theta$ from $\pi\left(\theta\right)$, the prior on $\theta$.
- Simulate data x using the model and parameters $\theta$.
- If $d(T(x), T(x∗)) \leq \epsilon$, accept $\theta$ as an observation from $\pi_{\epsilon}\left(\theta \vert x^{\ast}\right)$. Otherwise reject $\theta$.
- Repeat steps 1-3 until a sample of the required size has been obtained from $\pi_{\epsilon}\left(\theta \vert x^{\ast}\right)$ or a fixed number of iterations.
Note that in the case $\epsilon = 0$, the ABC algorithm reduces to a standard rejection algorithm, i.e. a Gibbs Sampler. Thus we accept not only those simulations which result in a summary statistic which agrees with $T(x^{\ast})$ but all those simulations within a distance $\epsilon$. There is a compromise in the choice of $\epsilon$: the larger $\epsilon$, the more efficient the algorithm is in terms of the acceptance probability but the greater the bias (the approximation in the posterior distribution). Choosing $\epsilon$ small is liable to have a large Monte-Carlo error because a small acceptance probability leads to a large variance of the corresponding estimator. This is because the number of accepted values, the sample used for estimating the parameter is small.
The Algorithm in Practice
A data set contains the genetic linkage of 197 animals, in which the animals are distributed into 4 categories, labeled 1 through to 4. Let $y_i$ denote the total number of animals in category i, and let $p_i$ be the probability that an animal belongs to category i, with $i=1,2,3,4$.
Suppose that $y = (y_1, y_2, y_3, y_4) = (125, 18, 20, 34)$, with category probabilities
\[(p1,p2,p3,p4) = \left(\left(\frac{1}{2} + \frac{\theta}{4}\right), \left(\frac{(1 - \theta)}{4}\right),\left(\frac{(1 - \theta)}{4}\right), \frac{\theta}{4} \right)\]We are interested in the posterior distribution of the parameter $\theta$. We assume $\theta \sim U\left(0,1\right)$. It is possible to show, with simple algebra, that the likelihood is
\[L\left( \theta \vert y \right) \propto \left(2+\theta\right)^{y_1}\left(1−\theta\right)^{y_2+y_3}\theta^{y_4}\]Therefore $(y_1, y_2 + y_3, y_4)$ are sufficient summary statistics. Note that it suffices to know $y_2 + y_3$ rather than the individual values $y_2$ and $y_3$.
Assume $d(x, y) = \sqrt{\sum_{i=1}^3(x_i − y_i)^2}$. Fix $\epsilon \geq 0$.
- Simulate $\theta$ from $U(0,1)$.
- Simulate data $x$ from Multinomial(197, p) where $p = (p1,p2,p3,p4)$ as defined above. Note that we have combined the probabilities for categories 2 and 3 for the previous argument on sufficient statistics.
- If $d(x, x^{\ast}) \leq \epsilon$, accept $\theta$ as an observation from $\pi_{\epsilon}\left(\theta \vert x^{\ast}\right)$. Otherwise reject $\theta$.
- Repeat steps 1-3 N times.
To perform this simulation using python, I have written a custom method called genetic_linkage that implements the ABC algorithm above. Please refer to the source file for details. The following table show the results for the first five iterations of the algorithm out of $N=100000$.
| theta | distance | |
|---|---|---|
| 0 | 0.771028 | 22.627417 |
| 1 | 0.492547 | 12.328828 |
| 2 | 0.248526 | 50.219518 |
| 3 | 0.087905 | 62.032250 |
| 4 | 0.205806 | 74.712783 |
The whole simulated $\theta$ and distance values are shown in the next plot:
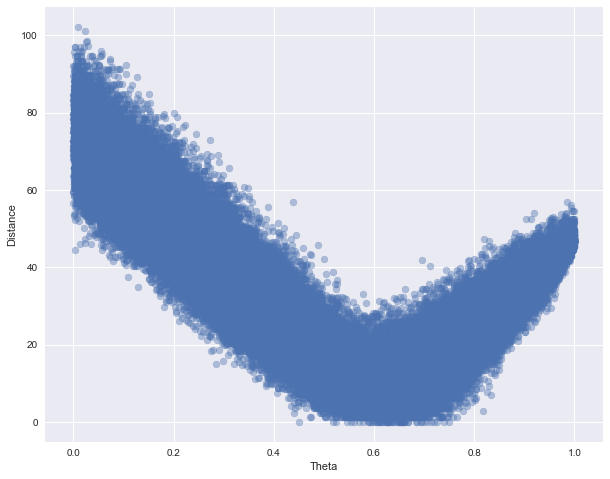
In 61 of the 100000 simulations we simulated data with the same sufficient statistic as the observed data. If we set $\epsilon = 3$, 1043 simulations are accepted. For $\epsilon = 3$, the mean and standard deviation of the (approximate) posterior distribution are 0.62 and 0.051, respectively. These results are in close agreement with the results we could obtained using the Gibbs sampler - if you are curious, try as an exercise.
Conclusions
In this post, we have understood the importance of ABC algorithms. The example we have used is however is extremely simple since the likelihood is tractable.
It should be noted that is not always possible to identify sufficient summary statistics, and it is prohibitive to use $x^{\ast}$. In such cases a second level of approximation is often used, where a summary statistic say $S(x)$ is used in place of $T(x)$. Generally, $S(x)$ is chosen to capture key features observed in the data and hopefully T(x) is close to being sufficient. However, unless $S(x)$ is a sufficient statistic there will be an associated error. We will see in a future post the use of such an approximate summary statistics with a genetic mutation model. If you have enjoyed this post, and you want to get more, please feel free to subscribe here!
References:
- Dempster et al (1977).Maximum Likelihood from Incomplete Data via the EM Algorithm
- Geman and Geman (1984). Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images.
- Hasting (1970). Monte Carlo sampling methods using Markov chains and their application.
- Tavare et al (1997). Inferring coalescence times from DNA sequence data.
