The Importance of Preprocessing in a Machine Learning Pipeline

Introduction

Scikit-learn, typically denoted as sklearn, is a very popular python library for Machine Learning. It is great, and it is de-facto the standard benchmark among Data Scientist. In this post, I would like to focus on a very important aspect related to the preprocessing phase (also known as dataset creation): the transformation of data.

Notably, people transform their data before training a model. However, from a technical point of view, people tend to confuse the process of scaling with the one of standardization. Here, I would like to shed lights on the distinction between the two, using the sklearn framework.

In general, sklearn can be divided into two major families of classes: estimators and transformers. Here, we will focus on the latter, since those are mainly used in the dataset creation phase. In particular, any transformer in sklearn is characterized by two methods:

• The .fit(), which is used to teach the transformer something about the data;
• The .transformer(), which uses what was learned to do the data transformation.

Why Scaling is very important

Scaling data is very useful, especially when features have different size and magnitude. Notably, this process improves the score of the model on the test set. To illustrate the problem, we use the well-known Boston Dataset: this dataset contains information collected by the U.S Census Service concerning housing in the area of Boston Mass. For more information on that, please visit the following website. To read this post, it is sufficient to know that this dataset has 506 rows and 14 column: the next Figure shows the statistical distribution of those features:

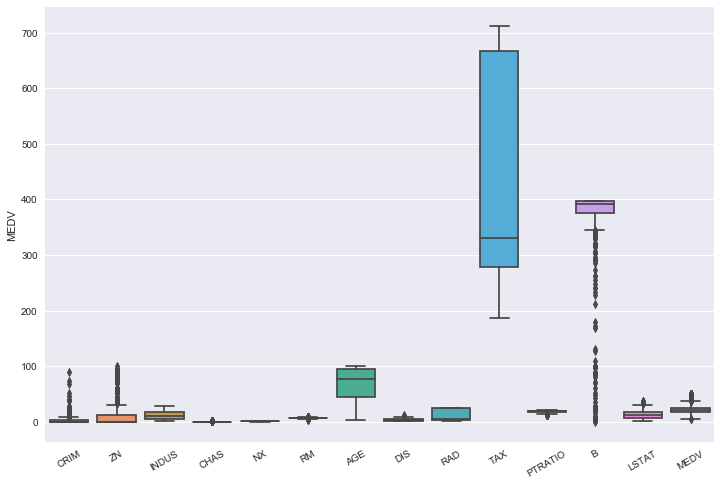
It is clear there exists an important variability among features due to the scaling effect: the magnitude on taxes is of thousands, whereas the one of age is, not surprisingly, of hundreds. Furthermore, most of them are are pretty skewed, and so it is good practice to scale them before fitting a model. Also, we do not know (a priori) which features might be considered important for our model, so scaling is a way to implicitly assign equal weight to different features that show different scale and magnitude: only after scaling we will pick the ones who explain our target the better.

Typically, to scale data we implement the StandardScaler method in sckit-learn.

Standard Scaler

To perform scaling of the data, we use the StandardScaler transformer. The process goes as follows:

• first, we initialize a StandardScaler();
• we then fit the scaler on the data;
• we then transform the original data in the scaled one.

This translates into the following python snippet:

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(boston)
X_scaled = scaler.transform(boston)

Hence,

• the .fit() learns the mean and and the scale of each feature;
• the .transform() standardizes the features using those mean and scale.

Note that we can directly use the fit_transform() on the data. However, please note that the latter must be used only on training data, whereas on new data, just use transform(). The fit_transform() is more computationally efficient than running firstly a .fit() and then the corresponding .transform() on the training data.

After scaling, the data looks like this:

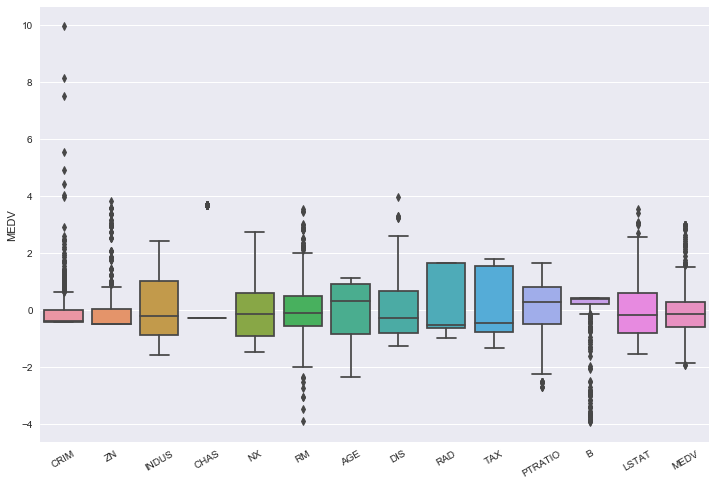
Force data to be Gaussian

The image is pretty clear: we have scaled the data, but still the data show the skewed we have observed in the original data. That means that the data have been reshaped in a different dimension, but the original relationship have been maintained.

A possibility is to force the data to be Gaussian (or at least more behaved). A way to make this is to use Power Transformations such as the well-known Box-Cox Transform, introduced by Box and Cox (1964), defined as follows:

\[BC_{\lambda}(x) = \begin{cases} \frac{x^{\lambda}-1}{\lambda} \quad \text{if} \quad \lambda \neq 0\\ \log(x) \quad \text{if} \quad \lambda = 0 \end{cases}\]

The idea is to raise your data x to some power, $\lambda$. Note, however, that this is only applicable to non-negative data points, so be careful when trying to applying this transformation: in principle, a good practice is to take the absolute value of your data, but this decision is up to the scientist. Alternatively, one can use the Yeo and Johnson (1997) power transformation, which accomodates for both positive and negative values.

from sklearn.preprocessing import PowerTransformer
pt = PowerTransformer(method='yeo-johnson')
data_gauss = pt.fit_transform(X_scaled)

The result is shown in the following figure:

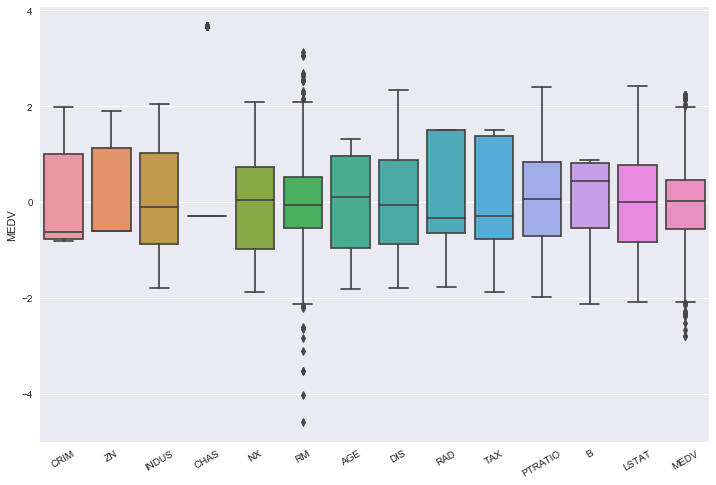
we clearly see that, for example, the features LSTAT and DIS looks more Gaussian than before.

Summing-up with the Feature Union Pipeline

One of the coolest thing about scikit-learn is the Pipeline object, which can be used to chain multiple estimators into one. Among several Pipelines, FeatureUnion is very useful in the preprocessing phase. It combines several transformer objects into a new transformer that combines their output. As noted in the official documentation,

A FeatureUnion takes a list of transformer objects. During fitting, each of these is fit to the data independently. For transforming data, the transformers are applied in parallel, and the sample vectors they output are concatenated end-to-end into larger vectors.

It is recommended using the FeatureUnion object for two reasons:

• Most of the data science projects require several steps of data preprocessing and transformation. With this FeatureUnion transformer, we do not need to perform multiple fit and transform, but just a single call.

• Using FeatureUnion improves efficiency in both the code and the runtime.

A simple implementation that sums up the aforementioned steps goes as follows:

from sklearn.pipeline import Pipeline
transformer = Pipeline(
    [
      ('scaler', StandardScaler()),
      ('pt', PowerTransformer(method='yeo-johnson')),
    ]
)
transformer = transformer.fit(boston)
results = transformer.transform(boston)

Conclusions

We have understood the importance of transformer in the sckit-learn framework, in particular on the scaler one. We also understood the difference between scaling and standardization. Obviously, scaling does not come from free: we have to consider the fact that we have to deal with the drawback of loosing some physical interpretability.

If you want to replicate the results seen in this post, please check the source code here.

References:

• Giussani (2020). Applied Machine Learning with Python.